¶ Introduction
The multipole expansion is a powerful mathematical technique used to approximate the electrostatic potential due to a localized charge distribution when the observation point lies far from the source region. In such cases, when , it is possible to expand the potential in a series of inverse powers of . Each term in this expansion corresponds to a distinct multipole moment of the charge distribution, capturing increasingly fine details of its spatial structure.
This approach is invaluable in both classical and astrophysical electrodynamics. It allows us to:
- Truncate the potential at low-order terms when higher-order structure is negligible (e.g., monopole or dipole approximations),
- Classify field behavior by symmetry and falloff rate ( for the -th multipole),
- Connect physical intuition about charge distributions to analytic representations of fields.
Physically, the first few terms have clear interpretations:
- The monopole term reflects the total charge.
- The dipole term accounts for the net separation of positive and negative charge.
- The quadrupole and higher-order terms describe finer angular structure in the distribution.
The multipole expansion is especially effective when solving boundary value problems, analyzing radiation fields at large distances, or evaluating the asymptotic behavior of potentials in astrophysical and molecular systems.
¶ Setup
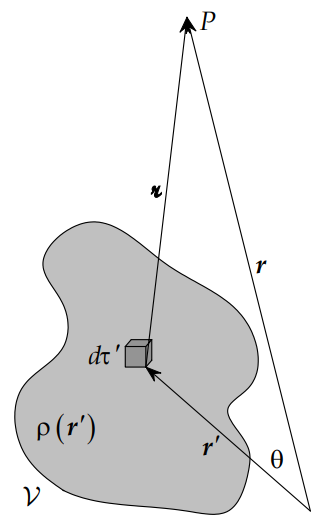
Recall the potential at point due to a charge distribution is given by the integral form of Coulomb's law:
where is the volume element at the source point , and where is the distance between the origin of our coordinate system and point as shown in the diagram.
¶ Derivation
Using the law of cosines, we can rewrite the denominator of the intergrand as
where is the angle between the vectors and .
This can now be simplified further by writing it as
with
In this form, it becomes obvious that if (we are looking at points far away from the source charges), than , thus warranting a binomial expansion:
Substituting our definition of back into the equation and grouping like powers of :
Interestingly, the coefficients are Legendre polynomials! Thus, we can cmopactly write this as
where are the Legendre polynomials. Thus, substituting this back into the potential integral, we arrive at
¶ Interpretation
This expression writes the potential as a sum over multipole moments of increasing order , each weighted by the corresponding Legendre polynomial.
- The term is the monopole moment (total charge),
- The term corresponds to the dipole moment,
- The term corresponds to the quadrupole moment,
- and so on.
The angle is the angle between the vectors (observation point) and (source point). Equivalently,
where hats denote unit vectors.
- This expansion converges when , that is, when the observation point is outside the charge distribution.
Each multipole term falls off with distance as , so that the corresponding electric field falls off as .
¶ Multipole Moments
Multipole moments are a sequence of scalar, vector, and tensor quantities that encode increasingly fine details of a charge distribution's spatial structure. In the context of the multipole expansion of the potential,
each term is associated with a distinct multipole moment. These moments, monopole, dipole, quadrupole, and higher, determine the angular and radial behavior of the potential and field far from the source.
¶ Monopole Moment
The monopole moment is simply the total charge:
In the far-field, this contributes the leading term of the potential:
This term dominates when there is net charge present, and it exhibits spherical symmetry.
¶ Dipole Moment
The dipole moment vector is defined as:
Physically, it measures the separation of positive and negative charges. It contributes the next term in the expansion when the net charge vanishes:
This potential has angular dependence and falls off as .
¶ Quadrupole Moment
The quadrupole moment tensor captures second-order deviations from spherical symmetry. It is defined as the symmetric, traceless tensor:
In practice, one often starts from the simpler (non-traceless) form:
The quadrupole term contributes a potential of the form:
This term becomes significant when both the total charge and the dipole moment vanish.
¶ Higher Multipole Moments
Higher-order moments () involve increasingly complex tensor structures:
- Octupole moment (rank-3 tensor):
- Hexadecapole moment (rank-4 tensor), etc.
In general, the -th multipole moment is a rank- Cartesian tensor constructed from integrals of times . These contributions fall off as .
¶ Physical Significance
- Monopole: Total charge — field resembles a point charge.
- Dipole: Directional separation of charge — field resembles a bar magnet or polar molecule.
- Quadrupole: Elongated charge distributions — e.g., dumbbell-shaped systems or symmetric configurations with zero dipole moment.
- Higher orders: Important in precision modeling of complex systems, such as atomic nuclei, planetary fields, and radiation patterns.
The vanishing of lower-order moments often reveals symmetries in the charge distribution.
¶ Example: Dipole Potential
Let consist of a pair of opposite charges and separated by a small distance . Then
and the far-field potential is approximately
This angular dependence is characteristic of dipole radiation and is critical in electrodynamics and antenna theory.
¶ Conclusion
Multipole moments provide a systematic way to approximate the fields of complex charge distributions. They offer deep physical insight into the structure and symmetries of the source and are widely used in electrostatics, astrophysics, quantum chemistry, and gravitational theory. In many cases, only the first few moments are needed to describe the system to high accuracy in the far field.
¶ References
- Griffiths, D. J. (1999). Introduction to Electrodynamics (3rd Edition). Prentice Hall. Example 3.10.
- Griffiths, D. J. (1999). Introduction to Electrodynamics (3rd ed.). Prentice Hall.
- Jackson, J. D. (1999). Classical Electrodynamics (3rd ed.). Wiley.